Introduction: The Orchestra of Hidden States

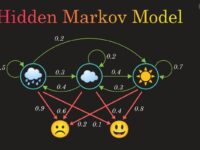
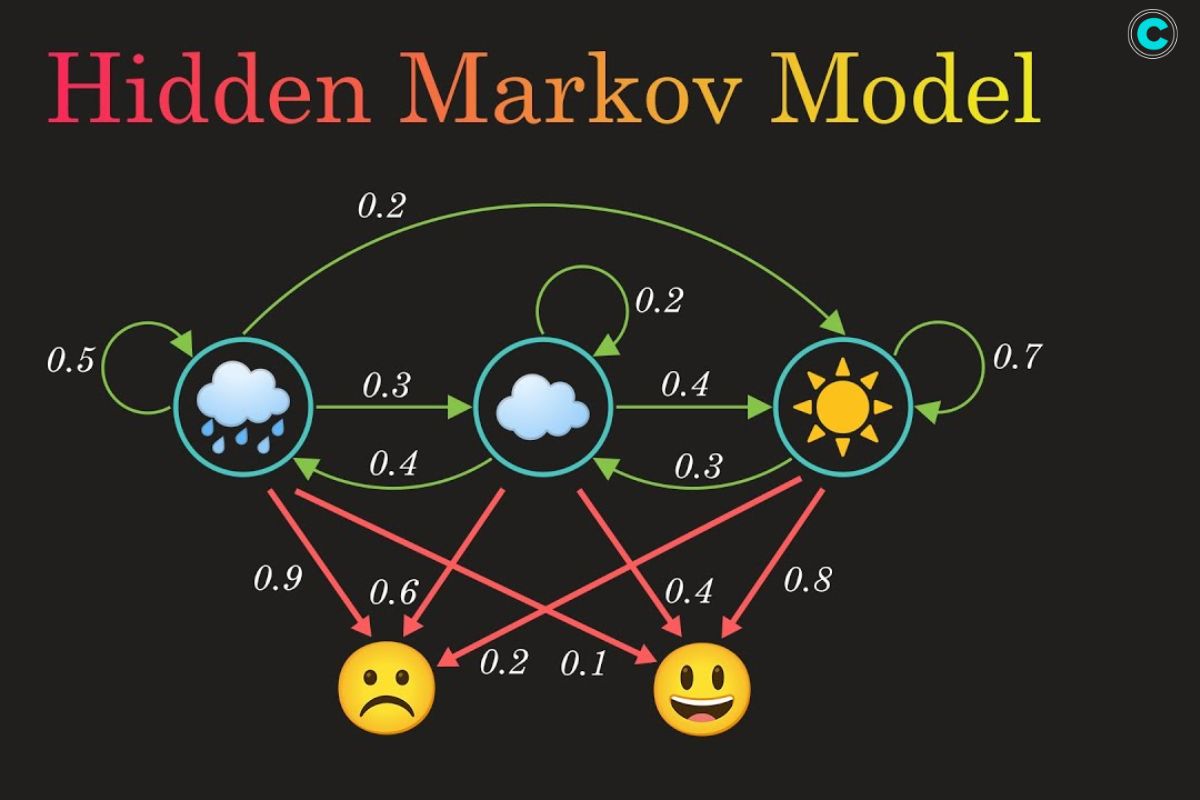
Imagine a symphony where the musicians play behind a curtain—you can’t see them, but you can hear their melodies and infer which instruments are playing. This unseen performance is much like the world of Hidden Markov Models (HMMs). In this orchestra, the hidden states are the invisible players (like “rainy” or “sunny” in a weather model), and the observations are the audible notes we can record (like seeing someone carry an umbrella).

In data-driven fields, such as speech recognition, bioinformatics, or stock market prediction, understanding these invisible states is crucial. But how do we train such a model when the hidden structure isn’t visible? Enter the Baum-Welch algorithm, also known as the Forward-Backward algorithm—a mathematical maestro that tunes the HMM parameters to fit the observed data perfectly.

The Hidden World: What Makes HMMs So Powerful

An HMM is like a storyteller weaving a tale of probabilities. Each scene (hidden state) leads to another with a certain chance, and each scene emits visible clues (observations). Yet, unlike simple models, HMMs allow for uncertainty—they acknowledge that we rarely see the full story.

The Baum-Welch algorithm empowers us to learn this hidden narrative. It’s a cornerstone in modern AI systems, quietly operating behind technologies like Google Voice, predictive text, and even gene sequencing tools.

For students exploring the mathematics of AI, mastering such algorithms is essential. If you’re enrolled in a data science course in Mumbai, you’ll encounter HMMs as a bridge between probability theory and machine learning—a place where math transforms into intelligent systems.

Unveiling the Secret: The Core Idea of Baum-Welch

The challenge with HMMs is circular: to know the hidden states, we must know the parameters; to know the parameters, we must know the hidden states. The Baum-Welch algorithm breaks this cycle through Expectation-Maximization (EM).

Think of EM as a detective and a craftsman working together:

• The Expectation step (E-step) guesses the hidden sequences based on current parameters.
• The Maximization step (M-step) refines those parameters based on the guessed sequences.

This process repeats, each iteration making the model more attuned to reality—like tuning an instrument by listening carefully to each note until it sounds just right.

The algorithm uses two fundamental processes:

1. Forward Pass – Calculates the probability of partial observation sequences up to a point.
2. Backward Pass – Works in reverse, calculating the likelihood of future observations given the current state.

Together, these two movements—forward and backward—create a complete harmonic loop, ensuring that the hidden symphony becomes clearer with each repetition.

Mathematical Rhythm: The Equations Behind the Music

At the heart of Baum-Welch lies elegant mathematics:

• Forward Probability (α): Probability of reaching a state at a given time considering past observations.
• Backward Probability (β): Probability of observing the remaining data from a given state.
• Gamma (γ): The expected proportion of time the model spends in a particular state.
• Xi (ξ): The expected transitions between states.

By combining these quantities, the algorithm updates transition probabilities (A), emission probabilities (B), and initial probabilities (π). Each update is like a musician fine-tuning pitch, rhythm, and tempo to synchronize with the ensemble.

Understanding this balance of probability and optimization is what transforms a model from abstract math to practical intelligence. Professionals aiming to master these algorithms can benefit from structured programs like a data scientist course, where theory meets application through hands-on problem-solving.

Real-World Resonance: From Speech to Genomics

The Baum-Welch algorithm isn’t just an academic curiosity—it’s the silent engine behind everyday intelligence. In speech recognition, it deciphers spoken words by mapping sounds to probable phonemes. In genomics, it reveals hidden biological patterns like gene boundaries. In finance, it models market behaviors that seem unpredictable yet follow probabilistic rhythms.

Each of these applications mirrors the same learning cycle—guess, refine, repeat—until the model’s hidden states align closely with reality. Much like a conductor learning to interpret a complex score, the algorithm refines its understanding until harmony emerges.

Learners pursuing a data science course in Mumbai often explore these applications firsthand, translating mathematical elegance into real-world impact.

Conclusion: From Hidden Notes to Mastered Melodies

The Baum-Welch algorithm reminds us that learning isn’t always about what we see—it’s about uncovering what lies beneath. In the landscape of machine learning, it acts as a translator between visible data and invisible patterns, bridging uncertainty with structure.

Much like a composer who listens to the faint echoes behind each note, data scientists rely on such algorithms to reveal meaning in chaos. Whether it’s decoding speech, predicting markets, or understanding DNA, HMMs and the Baum-Welch algorithm teach us that even the hidden has a rhythm—waiting patiently to be discovered by those who can hear it.

And for those embarking on a data scientist course, understanding this algorithm isn’t just about equations—it’s about learning how to listen to data’s secret music.

Business name: ExcelR- Data Science, Data Analytics, Business Analytics Course Training Mumbai

Address: 304, 3rd Floor, Pratibha Building. Three Petrol pump, Lal Bahadur Shastri Rd, opposite Manas Tower, Pakhdi, Thane West, Thane, Maharashtra 400602

Phone: 09108238354

Email: enquiry@excelr.com